Multiple Choice
Find the area of the largest rectangle that can be inscribed in the ellipse 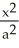 +
+ 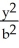 = 1.
= 1.
A) (3/2) ab square units
B) 2ab square units
C) 4ab square units
D) 2 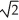 ab square units
ab square units
E) ab square units
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q88: The function f(x) = 4 + k
Q89: Evaluate the limit . <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q90: Determine the concavity of f(x) =
Q91: Which of the following statements best
Q92: A cylindrical can constructed from sheet metal
Q94: Find the maximum value of the function
Q95: A lamp is 3 metres high on
Q96: Find two nonnegative numbers whose sum is
Q97: Find the absolute maximum and absolute
Q98: Use Newton's Method to find the x