Solved

The Equation Y = Sin(x + Y) - Defines

Question 111

Multiple Choice

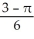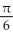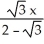
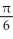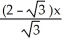
The equation y = sin(x + y) - The equation y = sin(x + y) - defines y as a function of x near the point . Find the linearization of that function at x = 0. A) L(x) = + B) L(x) = - C) L(x) = + D) L(x) = - E) L(x) = + (3 + 3) x defines y as a function of x near the point The equation y = sin(x + y) - defines y as a function of x near the point . Find the linearization of that function at x = 0. A) L(x) = + B) L(x) = - C) L(x) = + D) L(x) = - E) L(x) = + (3 + 3) x . Find the linearization of that function at x = 0.


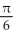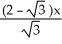
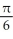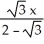
A) L(x) = The equation y = sin(x + y) - defines y as a function of x near the point . Find the linearization of that function at x = 0. A) L(x) = + B) L(x) = - C) L(x) = + D) L(x) = - E) L(x) = + (3 + 3) x + The equation y = sin(x + y) - defines y as a function of x near the point . Find the linearization of that function at x = 0. A) L(x) = + B) L(x) = - C) L(x) = + D) L(x) = - E) L(x) = + (3 + 3) x
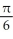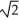B) L(x) = The equation y = sin(x + y) - defines y as a function of x near the point . Find the linearization of that function at x = 0. A) L(x) = + B) L(x) = - C) L(x) = + D) L(x) = - E) L(x) = + (3 + 3) x - The equation y = sin(x + y) - defines y as a function of x near the point . Find the linearization of that function at x = 0. A) L(x) = + B) L(x) = - C) L(x) = + D) L(x) = - E) L(x) = + (3 + 3) x
C) L(x) = The equation y = sin(x + y) - defines y as a function of x near the point . Find the linearization of that function at x = 0. A) L(x) = + B) L(x) = - C) L(x) = + D) L(x) = - E) L(x) = + (3 + 3) x + The equation y = sin(x + y) - defines y as a function of x near the point . Find the linearization of that function at x = 0. A) L(x) = + B) L(x) = - C) L(x) = + D) L(x) = - E) L(x) = + (3 + 3) x
D) L(x) = The equation y = sin(x + y) - defines y as a function of x near the point . Find the linearization of that function at x = 0. A) L(x) = + B) L(x) = - C) L(x) = + D) L(x) = - E) L(x) = + (3 + 3) x - The equation y = sin(x + y) - defines y as a function of x near the point . Find the linearization of that function at x = 0. A) L(x) = + B) L(x) = - C) L(x) = + D) L(x) = - E) L(x) = + (3 + 3) x
E) L(x) = The equation y = sin(x + y) - defines y as a function of x near the point . Find the linearization of that function at x = 0. A) L(x) = + B) L(x) = - C) L(x) = + D) L(x) = - E) L(x) = + (3 + 3) x + (3 The equation y = sin(x + y) - defines y as a function of x near the point . Find the linearization of that function at x = 0. A) L(x) = + B) L(x) = - C) L(x) = + D) L(x) = - E) L(x) = + (3 + 3) x + 3) x

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q106: Find the solution of the equation <img

Q107: The equation xy + <img

Q108: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Given that

Q109: What are the asymptotes of the graph

Q110: An open rectangular box with square base

Q112: Use linear approximation to approximate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"

Q113: Evaluate the limit <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate the

Q114: By considering the locations of its critical

Q115: Find the Taylor polynomial of degree 4

Q116: Find a linear approximation suitable for estimating