Multiple Choice
Find the inverse of the function f(x) = 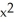 - 8x + 4, where x 4. State its domain.
- 8x + 4, where x 4. State its domain.
A) 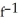 (x) = 4 -
(x) = 4 - 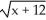 . Domain is x -12.
. Domain is x -12.
B) 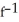 (x) = 4 +
(x) = 4 + 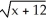 . Domain is x -12.
. Domain is x -12.
C) 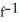 (x) = 4 +
(x) = 4 + 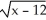 . Domain is x 12.
. Domain is x 12.
D) 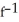 (x) = 4 -
(x) = 4 - 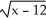 . Domain is x 12.
. Domain is x 12.
E) f(x) has no inverse.
Correct Answer:

Verified
Correct Answer:
Verified
Q44: Calculate and simplify the derivative of f(x)
Q45: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" =
Q46: Find y' if y = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q47: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="
Q48: The function f(x) = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q50: Find and simplify the derivative of <img
Q51: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find (173)
Q52: Find and simplify the derivative of <img
Q53: Find the general solution of the differential
Q54: Solve the logarithmic equation log x =