Solved

Find the Derivative of F(t) = (5t)

Question 29

Multiple Choice

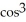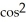Find the derivative of f(t) = Find the derivative of f(t) = (5t) . A) 15 (5t) sin(5t) B) -3 (5t) sin(5t) C) -15 (5t) sin(5t) D) 15 (5t) E) 3 (5t) (5t) .


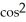A) 15 Find the derivative of f(t) = (5t) . A) 15 (5t) sin(5t) B) -3 (5t) sin(5t) C) -15 (5t) sin(5t) D) 15 (5t) E) 3 (5t) (5t) sin(5t)
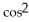B) -3 Find the derivative of f(t) = (5t) . A) 15 (5t) sin(5t) B) -3 (5t) sin(5t) C) -15 (5t) sin(5t) D) 15 (5t) E) 3 (5t) (5t) sin(5t)
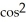C) -15 Find the derivative of f(t) = (5t) . A) 15 (5t) sin(5t) B) -3 (5t) sin(5t) C) -15 (5t) sin(5t) D) 15 (5t) E) 3 (5t) (5t) sin(5t)
D) 15 Find the derivative of f(t) = (5t) . A) 15 (5t) sin(5t) B) -3 (5t) sin(5t) C) -15 (5t) sin(5t) D) 15 (5t) E) 3 (5t) (5t)
E) 3 Find the derivative of f(t) = (5t) . A) 15 (5t) sin(5t) B) -3 (5t) sin(5t) C) -15 (5t) sin(5t) D) 15 (5t) E) 3 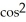(5t) (5t)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q24: If x sin y = cos (x

Q25: Find the equation of the straight line

Q26: A particle moves along the x-axis

Q27: Where does the normal line to the

Q28: Given g(x) = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Given g(x)

Q30: A ball is thrown vertically upward from

Q31: Differentiate y = sin 4x.<br>A) 2cos 4x<br>B)

Q32: Find an equation of the line tangent

Q33: An object moves in a straight line

Q34: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find if