Solved

Given F(x) = - 6x +12, Find the Value

Question 74

Multiple Choice

Given f(x) = 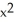Given f(x) = - 6x +12, find the value of c in the open interval (4, 7) that satisfies . A) B) C) 5 D) 6 E) - 6x +12, find the value of c in the open interval (4, 7) that satisfies Given f(x) = - 6x +12, find the value of c in the open interval (4, 7) that satisfies . A) B) C) 5 D) 6 E) .


A) Given f(x) = - 6x +12, find the value of c in the open interval (4, 7) that satisfies . A) B) C) 5 D) 6 E)
B) Given f(x) = - 6x +12, find the value of c in the open interval (4, 7) that satisfies . A) B) C) 5 D) 6 E)
C) 5
D) 6
E) Given f(x) = - 6x +12, find the value of c in the open interval (4, 7) that satisfies 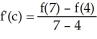. A) 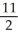B) 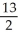C) 5 D) 6 E)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q69: Find an equation of the line tangent

Q70: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate 5

Q71: A spherical balloon is being inflated.

Q72: Let f(x) be a function such that

Q73: Let y = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let y

Q75: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find if

Q76: let y = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="let y

Q77: There are lines that pass through the

Q78: Find the slope of the tangent line

Q79: Where is the function f(x) =