Solved

(X) = -Cos(4x) + 34, (X) = 2

Question 16

True/False

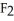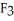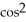(x) = -cos(4x) + 34, (x) = 2 (2x) - 15, and (x) = 7 -2 (2x) are all antiderivatives of f(x) = 8 sin(2x) cos(2x). (x) = -cos(4x) + 34, (x) = -cos(4x) + 34, (x) = 2 (2x) - 15, and (x) = 7 -2 (2x) are all antiderivatives of f(x) = 8 sin(2x) cos(2x). (x) = 2 (x) = -cos(4x) + 34, (x) = 2 (2x) - 15, and (x) = 7 -2 (2x) are all antiderivatives of f(x) = 8 sin(2x) cos(2x). (2x) - 15, and (x) = -cos(4x) + 34, (x) = 2 (2x) - 15, and (x) = 7 -2 (2x) are all antiderivatives of f(x) = 8 sin(2x) cos(2x). (x) = 7 -2 (x) = -cos(4x) + 34, (x) = 2 (2x) - 15, and (x) = 7 -2 (2x) are all antiderivatives of f(x) = 8 sin(2x) cos(2x). (2x) are all antiderivatives of f(x) = 8 sin(2x) cos(2x).

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q11: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate dx.

Q12: The population (in thousands) of the city

Q13: Use implicit differentiation to find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"

Q14: Determine the open intervals on the

Q15: Find an equation of the line tangent

Q17: Where does the function f(x) = <img

Q18: Find an equation of the line tangent

Q19: If f'(x) = 0 at every point

Q20: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find

Q21: Determine the open intervals on the