A Biologist Measures the Amount of Contaminant in a Lake

Short Answer

A biologist measures the amount of contaminant in a lake 5 hours after a chemical spill and again 8 hours after the spill. She sets up two possible models to determine Q, the amount of the chemical remaining in the lake as a function of t, the time in hours since the spill. The first model assumes the contaminant is leaving the lake at a constant rate, which she determines to be 3 tons/hour. Using this model, she estimates that the lake will be free from the contaminant 30 hours after the spill. Thus, 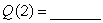and 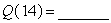. The second model assumes that the amount of contaminant decreases exponentially. In this model, she finds that 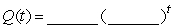. Round both answers to 3 decimal places.