Solved

In Certain Cases, There Is a Nonzero Vector

Question 33

Short Answer

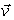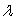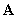In certain cases, there is a nonzero vector In certain cases, there is a nonzero vector and a scalar for a matrix such that . The vector is called an eigenvector of with eigenvalue . Let with eigenvector . What is its eigenvalue? and a scalar In certain cases, there is a nonzero vector and a scalar for a matrix such that . The vector is called an eigenvector of with eigenvalue . Let with eigenvector . What is its eigenvalue? 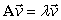for a matrix In certain cases, there is a nonzero vector and a scalar for a matrix such that . The vector is called an eigenvector of with eigenvalue . Let with eigenvector . What is its eigenvalue? 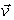such that In certain cases, there is a nonzero vector and a scalar for a matrix such that . The vector is called an eigenvector of with eigenvalue . Let with eigenvector . What is its eigenvalue? . 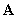The vector In certain cases, there is a nonzero vector and a scalar for a matrix such that . The vector is called an eigenvector of with eigenvalue . Let with eigenvector . What is its eigenvalue? 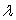is called an eigenvector of In certain cases, there is a nonzero vector and a scalar for a matrix such that . The vector is called an eigenvector of with eigenvalue . Let with eigenvector . What is its eigenvalue? 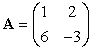with eigenvalue In certain cases, there is a nonzero vector and a scalar for a matrix such that . The vector is called an eigenvector of with eigenvalue . Let with eigenvector . What is its eigenvalue? . 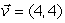Let In certain cases, there is a nonzero vector and a scalar for a matrix such that . The vector is called an eigenvector of with eigenvalue . Let with eigenvector . What is its eigenvalue? with eigenvector In certain cases, there is a nonzero vector and a scalar for a matrix such that . The vector is called an eigenvector of with eigenvalue . Let with eigenvector . What is its eigenvalue? . What is its eigenvalue?

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q28: A retailer's total monthly sales of three

Q29: Jack and Jill begin walking away from

Q30: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10073/.jpg" alt="Given that

Q31: For what value of x are

Q32: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10073/.jpg" alt="Let

Q34: The vector starting at the point P

Q35: Find the length of the vector

Q36: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10073/.jpg" alt="Let be

Q37: A country has two main political parties.

Q38: Let the vector <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10073/.jpg" alt="Let