Consider a Block (8x8 Pixels) of an Image as Shown $8 \times 8$

Essay

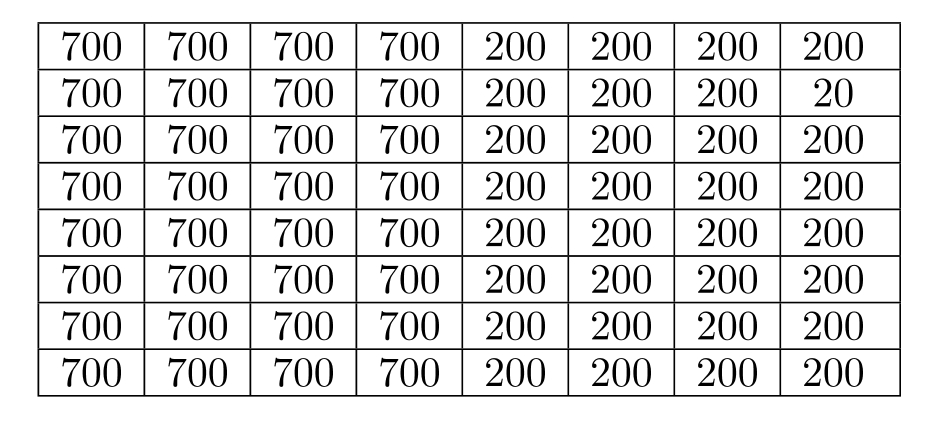
Consider a block (8x8 pixels) of an image as shown below. In a particular color plane, the pixel values are as follows:

A standard 2-D DCT for an $8 \times 8$ block size is defined as
$$F(u, v)=\frac{C(u) C(v)}{4} \sum_{i=0}^{7} \sum_{j=0}^{7} \cos \frac{(2 i+1) \cdot u \pi}{16} \cos \frac{(2 j+1) \cdot v \pi}{16} f(i, j),$$
where $i, j, u, v$ are in $0 . .7$ , and the constants $C(u)$ and $C(v)$ are determined by
$$C(\xi)=\left\{\begin{array}{cl}\frac{\sqrt{2}}{2} & \text { if } \xi=0 \\1 & \text { otherwise. }\end{array}\right.$$
Suppose we compute a DCT $F(u, v)$ , where $u$ is rows and $v$ is columns.
(a) What value does $F(0,0)$ have? Explain.
(b) Describe the contents (roughly) of the other components. Explain.
Hint: Just thinking about it, rather than calculating everything, will save you time. What are values $F(u, 0)$ . What are values $F(0, v)$ .
What are other values $F(u, v)$ .