Solved

Transform the Function into a New Function by Stretching

Question 73

Essay

Transform the function Transform the function into a new function by stretching by a factor of 3 and reflecting across the x-axis, and then shifting the result down 3 units. Find the equation of . into a new function Transform the function into a new function by stretching by a factor of 3 and reflecting across the x-axis, and then shifting the result down 3 units. Find the equation of . by stretching Transform the function into a new function 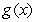by stretching by a factor of 3 and reflecting across the x-axis, and then shifting the result down 3 units. Find the equation of . by a factor of 3 and reflecting across the x-axis, and then shifting the result down 3 units. Find the equation of . Transform the function into a new function by stretching by a factor of 3 and reflecting across the x-axis, and then shifting the result down 3 units. Find the equation of .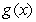

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q68: A free falling body has an initial

Q69: Find the minimum value of the function

Q70: Find the vertex of the parabola <img

Q71: Create a quadratic equation of the form

Q72: Convert the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9987/.jpg" alt="Convert the

Q74: For the quadratic function pictured determine the

Q75: Determine whether this parabola is concave up

Q76: Convert the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9987/.jpg" alt="Convert the

Q77: Find a for the parabola <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9987/.jpg"

Q78: The daily profit (f), in dollars, of