Multiple Choice
In the model ln(y) = 0 + 1x + , the predicted value is 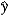 = exp (b0 + b1x +
= exp (b0 + b1x + 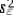 ÷ 2) . What is the impact of the estimated slope coefficient?
÷ 2) . What is the impact of the estimated slope coefficient?
A) b1 measures the approximate change in 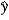 when x increases by 1 unit.
when x increases by 1 unit.
B) b1 × 0.01 measures the approximate change in 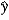 when x increases by 1%.
when x increases by 1%.
C) b1 measures the approximate change in 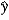 when x increases by 1%.
when x increases by 1%.
D) b1 × 100 measures the approximate change in 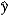 when x increases by 1 unit.
when x increases by 1 unit.
Correct Answer:

Verified
Correct Answer:
Verified
Q24: A variable with a value of x<sub>1</sub>x<sub>2</sub>
Q25: In cross-validation, if k equals the sample
Q26: An estimated linear regression of annual fuel
Q27: The following table contains the parameter
Q28: A study was completed on cholesterol in
Q30: The following table contains the parameter
Q31: Todd uses the quadratic regression model to
Q32: In a regression model with two
Q33: An estimated linear regression of annual fuel
Q34: In the following logarithmic regression model,