Solved

CNBC (2018) Reported 58% of Households Are Using Streaming Services

Question 28

Multiple Choice

CNBC (2018) reported 58% of households are using streaming services compared to standard cable. What are the expected value and the standard error of the sample proportion derived from a random sample of 500?


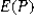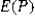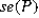A) CNBC (2018) reported 58% of households are using streaming services compared to standard cable. What are the expected value and the standard error of the sample proportion derived from a random sample of 500? A) = 0.42 and <em> </em> = 0.0221< / p> B) = 0.0221 and <em> </em> = 0.42< / p> C) = 0.58 and <em> </em> = 0.0221< / p> D) = 0.7615 and <em> </em> = 0.0341< / p> = 0.42 and <em> CNBC (2018) reported 58% of households are using streaming services compared to standard cable. What are the expected value and the standard error of the sample proportion derived from a random sample of 500? A) = 0.42 and <em> </em> = 0.0221< / p> B) = 0.0221 and <em> </em> = 0.42< / p> C) = 0.58 and <em> </em> = 0.0221< / p> D) = 0.7615 and <em> </em> = 0.0341< / p> </em> = 0.0221< / p>
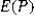B) CNBC (2018) reported 58% of households are using streaming services compared to standard cable. What are the expected value and the standard error of the sample proportion derived from a random sample of 500? A) = 0.42 and <em> </em> = 0.0221< / p> B) = 0.0221 and <em> </em> = 0.42< / p> C) = 0.58 and <em> </em> = 0.0221< / p> D) = 0.7615 and <em> </em> = 0.0341< / p> = 0.0221 and <em> CNBC (2018) reported 58% of households are using streaming services compared to standard cable. What are the expected value and the standard error of the sample proportion derived from a random sample of 500? A) = 0.42 and <em> </em> = 0.0221< / p> B) = 0.0221 and <em> </em> = 0.42< / p> C) = 0.58 and <em> </em> = 0.0221< / p> D) = 0.7615 and <em> </em> = 0.0341< / p> </em> = 0.42< / p>
C) CNBC (2018) reported 58% of households are using streaming services compared to standard cable. What are the expected value and the standard error of the sample proportion derived from a random sample of 500? A) = 0.42 and <em> </em> = 0.0221< / p> B) = 0.0221 and <em> </em> = 0.42< / p> C) = 0.58 and <em> </em> = 0.0221< / p> D) = 0.7615 and <em> </em> = 0.0341< / p> = 0.58 and <em> CNBC (2018) reported 58% of households are using streaming services compared to standard cable. What are the expected value and the standard error of the sample proportion derived from a random sample of 500? A) = 0.42 and <em> </em> = 0.0221< / p> B) = 0.0221 and <em> </em> = 0.42< / p> C) = 0.58 and <em> </em> = 0.0221< / p> D) = 0.7615 and <em> </em> = 0.0341< / p> </em> = 0.0221< / p>
D) CNBC (2018) reported 58% of households are using streaming services compared to standard cable. What are the expected value and the standard error of the sample proportion derived from a random sample of 500? A) = 0.42 and <em> </em> = 0.0221< / p> B) = 0.0221 and <em> </em> = 0.42< / p> C) = 0.58 and <em> </em> = 0.0221< / p> D) = 0.7615 and <em> </em> = 0.0341< / p> = 0.7615 and <em> CNBC (2018) reported 58% of households are using streaming services compared to standard cable. What are the expected value and the standard error of the sample proportion derived from a random sample of 500? A) = 0.42 and <em> </em> = 0.0221< / p> B) = 0.0221 and <em> </em> = 0.42< / p> C) = 0.58 and <em> </em> = 0.0221< / p> D) = 0.7615 and <em> </em> = 0.0341< / p> </em> = 0.0341< / p>

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q23: Many sample sizes can be drawn from

Q24: In a sample of 23 iPhones, 10

Q25: The population proportion p is the essential

Q26: In a population set, 14 students of

Q27: The Central Limit Theorem, by definition,

Q29: In a World Atlas study, 10% of

Q30: If the confidence coefficient is 0.77,

Q31: In a population set, 13 students of

Q32: A range of values used to estimate

Q33: What is the expected value of the