Solved

The Tenth Term in a Geometric Sequence Is 1,000,000,000

Question 32

Multiple Choice

The tenth term in a geometric sequence is 1,000,000,000. The common ratio is 10.
-Find a formula for the nth term of the seqence.


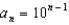
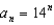
A) The tenth term in a geometric sequence is 1,000,000,000. The common ratio is 10. -Find a formula for the nth term of the seqence. A) B) C) D) E) None of these
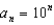
B) The tenth term in a geometric sequence is 1,000,000,000. The common ratio is 10. -Find a formula for the nth term of the seqence. A) B) C) D) E) None of these
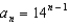
C) The tenth term in a geometric sequence is 1,000,000,000. The common ratio is 10. -Find a formula for the nth term of the seqence. A) B) C) D) E) None of these
D) The tenth term in a geometric sequence is 1,000,000,000. The common ratio is 10. -Find a formula for the nth term of the seqence. A) B) C) D) E) None of these
E) None of these

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q27: Evaluate the partial sum of the geometric

Q28: For all the problems in this set

Q29: Evaluate the infinite geometric series.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10230/.jpg" alt="Evaluate

Q30: Evaluate: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10230/.jpg" alt="Evaluate: A)

Q31: Do not use Pascal's Triangle.<br>-Identify the number

Q33: For all the problems in this set

Q34: Do not use Pascal's Triangle.<br>-Evaluate: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10230/.jpg"

Q35: For all the problems in this set

Q36: For all the problems in this set

Q37: The function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10230/.jpg" alt="The function