Solved

For All the Problems in This Set the Domain Is

Question 18

Multiple Choice

For all the problems in this set the domain is the set of positive integers.
Find a formula for the nth term of the arithmetic sequence.
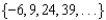
-For all the problems in this set the domain is the set of positive integers. Find a formula for the nth term of the arithmetic sequence. - A) B) C) D) E) None of these


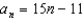
A) For all the problems in this set the domain is the set of positive integers. Find a formula for the nth term of the arithmetic sequence. - A) B) C) D) E) None of these
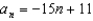
B) For all the problems in this set the domain is the set of positive integers. Find a formula for the nth term of the arithmetic sequence. - A) B) C) D) E) None of these
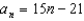
C) For all the problems in this set the domain is the set of positive integers. Find a formula for the nth term of the arithmetic sequence. - A) B) C) D) E) None of these
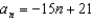
D) For all the problems in this set the domain is the set of positive integers. Find a formula for the nth term of the arithmetic sequence. - A) B) C) D) E) None of these
E) None of these

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q13: The tenth term in a geometric sequence

Q14: For all the problems in this set

Q15: Use Pascal's Triangle and the binomial theorem

Q16: Expand the expression. Use Pascal's Triangle to

Q17: The expression <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10230/.jpg" alt="The expression

Q19: Find the common ratio, r, of the

Q20: For all the problems in this set

Q21: For all the problems in this set

Q22: Which of the following sequences is geometric?<br>A)

Q23: Find the common ratio, r, of the