Solved

For All the Problems in This Set the Domain Is

Question 24

Multiple Choice

For all the problems in this set the domain is the set of positive integers.
Each of the sequences is arithmetic. Find the formula for the nth term.
-The 3rd term is 29. The 7th term is 57.


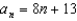
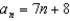
A) For all the problems in this set the domain is the set of positive integers. Each of the sequences is arithmetic. Find the formula for the nth term. -The 3rd term is 29. The 7th term is 57. A) B) C) D) E) None of these
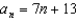
B) For all the problems in this set the domain is the set of positive integers. Each of the sequences is arithmetic. Find the formula for the nth term. -The 3rd term is 29. The 7th term is 57. A) B) C) D) E) None of these
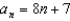
C) For all the problems in this set the domain is the set of positive integers. Each of the sequences is arithmetic. Find the formula for the nth term. -The 3rd term is 29. The 7th term is 57. A) B) C) D) E) None of these
D) For all the problems in this set the domain is the set of positive integers. Each of the sequences is arithmetic. Find the formula for the nth term. -The 3rd term is 29. The 7th term is 57. A) B) C) D) E) None of these
E) None of these

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q19: Find the common ratio, r, of the

Q20: For all the problems in this set

Q21: For all the problems in this set

Q22: Which of the following sequences is geometric?<br>A)

Q23: Find the common ratio, r, of the

Q25: For all the problems in this set

Q26: For all the problems in this set

Q27: Evaluate the partial sum of the geometric

Q28: For all the problems in this set

Q29: Evaluate the infinite geometric series.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10230/.jpg" alt="Evaluate