Multiple Choice
Find the inverse of the function.
-f(x) = 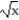 - 4, x 0
- 4, x 0
A) f-1(x) = x + 4, x 4
B) f-1(x) = 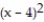
C) f-1(x) = - 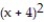 , x 4
, x 4
D) f-1(x) = 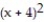 , x 4
, x 4
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q74: Find a formula for the function graphed.<br>-<img
Q75: Determine an appropriate viewing window for the
Q76: Solve for the angle θ, where
Q77: Find the domain and range of
Q78: State the period of the function
Q80: Determine whether or not the graph is
Q81: Choose the graph that matches the function.<br>-f(x)
Q82: Find the domain and graph the
Q83: Simplify the difference quotients <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Simplify
Q84: Is the function graphed one-to-one?<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Is