Multiple Choice
Solve for the angle θ, where 0 ≤ θ ≤ 2π
-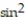 =
= 
A) = 0, , 2
B) 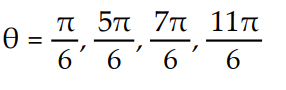
C) 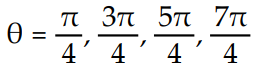
D) 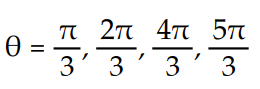
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q170: Simplify the difference quotients <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Simplify
Q171: Solve the problem. <br>-The distance an object
Q172: Evaluate or simplify the given expression.<br>-sin(2 <img
Q173: Graph the inverse of the function plotted,
Q174: Find the inverse of the function.<br>-f(x) =
Q176: Find the domain and range of
Q177: Find the exact value of the trigonometric
Q178: Solve the problem.<br>-The figure shown here shows
Q179: Graph the function. Determine the symmetry, if
Q180: Solve the problem.<br>-Let g(x) = x +