Multiple Choice
Graph the equation. Include the coordinates of any local extreme points and inflection points.
-y = x + cos 2x, 0 x 
A) 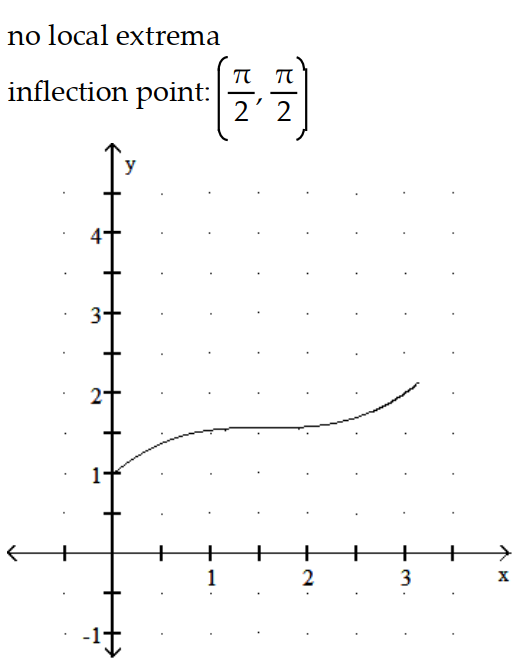
B) 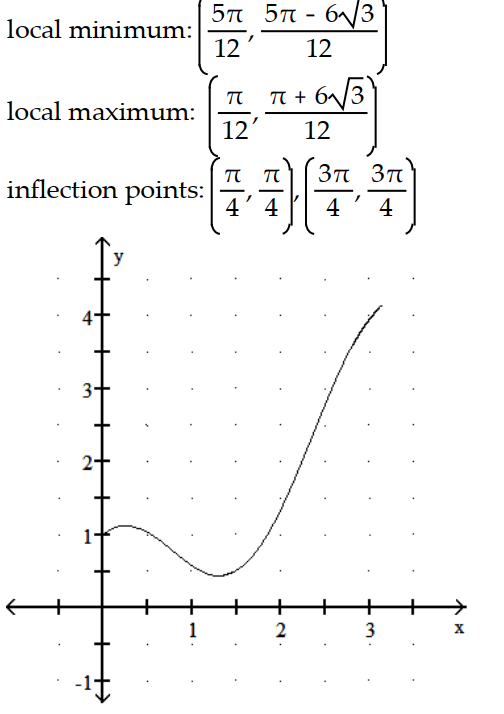
C) 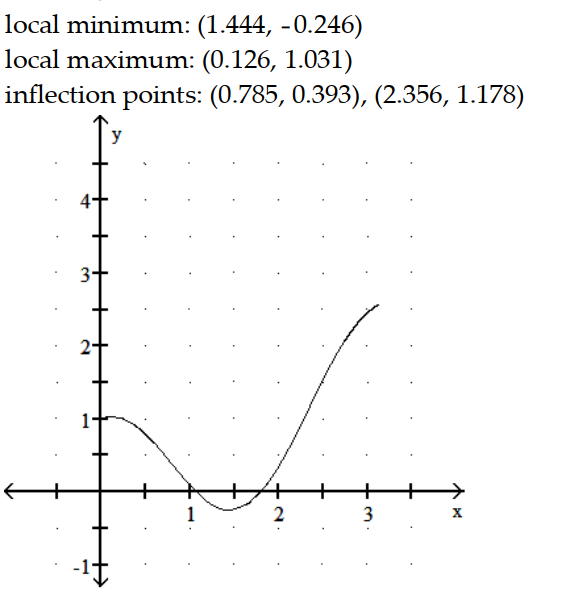
D) 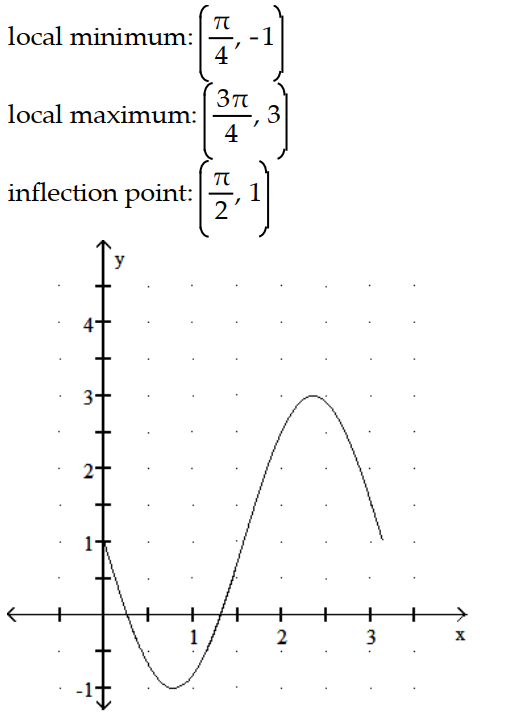
Correct Answer:

Verified
Correct Answer:
Verified
Q29: Use differentiation to determine whether the integral
Q30: Choose the one alternative that best completes
Q31: Solve the initial value problem. <br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg"
Q32: Find the largest open interval where
Q33: Solve the problem.<br>-The graphs below show the
Q35: Solve the problem. <br>-Given the velocity and
Q36: Solve the problem.<br>-The graphs below show the
Q37: Use differentiation to determine whether the integral
Q38: Provide an appropriate response. <br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg"
Q39: L'Hopital's rule does not help with