Find All the Roots of the Function $\approx$ 0128994, 2 $\approx$ 0351105, 2

Multiple Choice

Find all the roots of the function. Use preliminary analysis and graphing to determine good initial approximations. Round to six decimal places.
-f(x) = ln( 2x) - 2 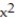+ 3x + 1

A) x $\approx$ 0.128994, 2.082514
B) x $\approx$ 0.351105, 2.304625
C) x $\approx$ 0.129105, 2.082625
D) x $\approx$ 1.629105, 3.582625