Solve the Problem $\pi$ ( 5 + Ln 6)
B) 2 $\pi$

Multiple Choice

Solve the problem.
-Find the volume of the solid generated by revolving the region in the first quadrant bounded by the coordinate axes, the curve y = 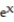, and the line x = ln 6 about the line x = ln 6.

A) 2 $\pi$ ( 5 + ln 6)
B) 2 $\pi$ ( 5 - ln 6)
C) 2 $\pi$ ( 6 - ln 6)
D) 2 $\pi$ (6 - ln 7)