Multiple Choice
Solve the problem.
-Find the volume of the solid generated by revolving the region in the first quadrant bounded by the coordinate axes, the curve y = 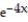 , and the line x = 3 about the y-axis.
, and the line x = 3 about the y-axis.
A) 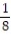 (1 - 11
(1 - 11 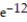 )
)
B) 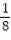 (1 - 12
(1 - 12 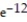 )
)
C) - 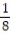 (1 + 13
(1 + 13 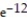 )
)
D) 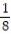 (1 - 13
(1 - 13 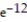 )
)
Correct Answer:

Verified
Correct Answer:
Verified
Q231: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.
Q232: Express the integrand as a sum of
Q233: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.
Q234: Find the surface area or volume.<br>-Use an
Q235: Solve the problem.<br>-Find the volume of
Q237: Solve the problem.<br>-Find the volume of
Q238: Evaluate the integral by using a substitution
Q239: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.
Q240: Express the integrand as a sum of
Q241: Integrate the function.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Integrate the function.