Multiple Choice
Find the volume.
-Find the volume of the solid generated by revolving the region in the first quadrant under the curve 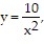 bounded on the left by x = 1, about the x-axis.
bounded on the left by x = 1, about the x-axis.
A) 100
B) 2
C) 10
D) 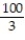
Correct Answer:

Verified
Correct Answer:
Verified
Q47: Choose the one alternative that best completes
Q48: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.
Q49: Solve the problem.<br>-Suppose that the accompanying table
Q50: Evaluate the integral by using a substitution
Q51: Express the integrand as a sum of
Q53: Solve the problem.<br>-Find the area of
Q54: Evaluate the improper integral or state that
Q55: Use reduction formulas to evaluate the integral.<br>-<img
Q56: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.
Q57: Use reduction formulas to evaluate the integral.<br>-<img