Solved

Find the Gradient Field F of the Function F

Question 160

Multiple Choice

Find the gradient field F of the function f.
-f(x, y, z) = Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D) Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D) + Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D)


A)
Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D)
B)
Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D)
C)
Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D)
D)
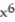
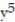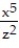
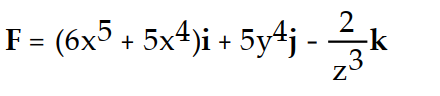
Find the gradient field F of the function f. -f(x, y, z) = + A) B) 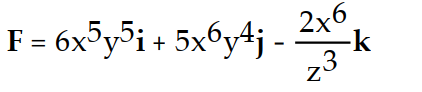C) 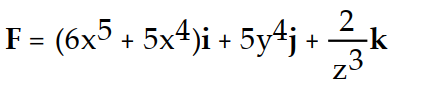D)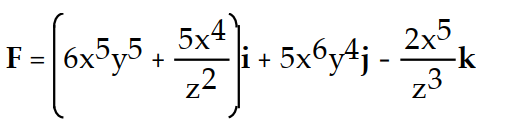

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q155: Find the flux of the vector

Q156: Use Stokes' Theorem to calculate the circulation

Q157: Apply Green's Theorem to evaluate the integral.<br>-<img

Q158: Find the flux of the vector field

Q159: Parametrize the surface S.<br>-S is the portion

Q161: Calculate the area of the surface

Q162: Evaluate the work done between point 1

Q163: Find the surface area of the

Q164: Find the divergence of the field F.<br>-F

Q165: Evaluate the line integral along the curve