Solved

Find the Gradient Field F of the Function F

Question 92

Multiple Choice

Find the gradient field F of the function f.
-f(x, y, z) = Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D) Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D) + Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D) Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D)


A) Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D)
B) Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D)
C) Find the gradient field F of the function f. -f(x, y, z) = + A) B) C) D)
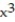
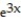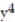
D) Find the gradient field F of the function f. -f(x, y, z) = + A) 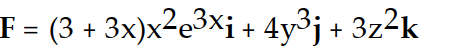B) 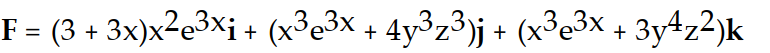C) 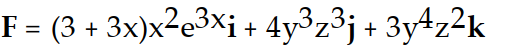D)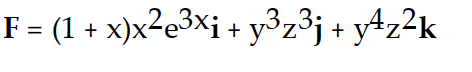

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q87: Find the surface area of the

Q88: Find the flux of the vector field

Q89: Find the work done by F

Q90: Find the mass of the wire

Q91: Using Green's Theorem, find the outward flux

Q93: Solve the problem.<br>-The shape and density

Q94: Evaluate the surface integral of G

Q95: Solve the problem.<br>-The shape and density

Q96: Evaluate the surface integral of the function

Q97: Using Green's Theorem, find the outward flux