Solved

Find the Gradient Field F of the Function F

Question 16

Multiple Choice

Find the gradient field F of the function f.
-f(x, y, z) = ln ( Find the gradient field F of the function f. -f(x, y, z) = ln ( + + ) A) B) C) D) + Find the gradient field F of the function f. -f(x, y, z) = ln ( + + ) A) B) C) D) + Find the gradient field F of the function f. -f(x, y, z) = ln ( + + ) A) B) C) D) )


A) Find the gradient field F of the function f. -f(x, y, z) = ln ( + + ) A) B) C) D)
B) Find the gradient field F of the function f. -f(x, y, z) = ln ( + + ) A) B) C) D)
C) Find the gradient field F of the function f. -f(x, y, z) = ln ( + + ) A) B) C) D)
D) Find the gradient field F of the function f. -f(x, y, z) = ln ( 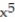+ + 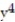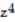) A) 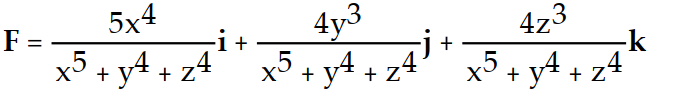B) 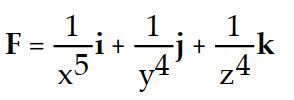C) 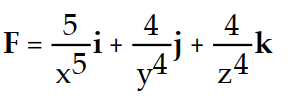D)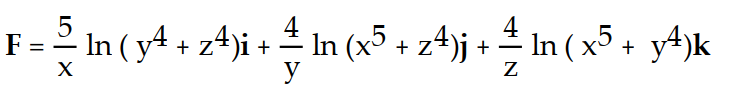

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q11: Calculate the circulation of the field

Q12: Find the potential function f for the

Q13: Using the Divergence Theorem, find the

Q14: Using Green's Theorem, compute the counterclockwise

Q15: Parametrize the surface S.<br>-S is the portion

Q17: Calculate the flux of the field F

Q18: Evaluate the surface integral of the function

Q19: Find the potential function f for the

Q20: Using the Divergence Theorem, find the

Q21: Find the potential function f for the