Solved

Use Stokes' Theorem to Calculate the Circulation of the Field π\pi

Question 43

Multiple Choice

Use Stokes' Theorem to calculate the circulation of the field F around the curve C in the indicated direction.
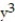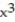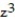-F = -9 Use Stokes' Theorem to calculate the circulation of the field F around the curve C in the indicated direction. -F = -9 i + 9 j + 4 k ; C: the portion of the paraboloid + = z cut by the cylinder A) - 2187 \pi B) 2187 /2 \pi C) - 2187 /2 \pi D) 2187 \pi i + 9 Use Stokes' Theorem to calculate the circulation of the field F around the curve C in the indicated direction. 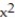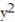-F = -9 i + 9 j + 4 k ; C: the portion of the paraboloid + = z cut by the cylinder A) - 2187 \pi B) 2187 /2 \pi C) - 2187 /2 \pi D) 2187 \pi j + 4 Use Stokes' Theorem to calculate the circulation of the field F around the curve C in the indicated direction. 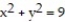-F = -9 i + 9 j + 4 k ; C: the portion of the paraboloid + = z cut by the cylinder A) - 2187 \pi B) 2187 /2 \pi C) - 2187 /2 \pi D) 2187 \pi k ; C: the portion of the paraboloid Use Stokes' Theorem to calculate the circulation of the field F around the curve C in the indicated direction. -F = -9 i + 9 j + 4 k ; C: the portion of the paraboloid + = z cut by the cylinder A) - 2187 \pi B) 2187 /2 \pi C) - 2187 /2 \pi D) 2187 \pi + Use Stokes' Theorem to calculate the circulation of the field F around the curve C in the indicated direction. -F = -9 i + 9 j + 4 k ; C: the portion of the paraboloid + = z cut by the cylinder A) - 2187 \pi B) 2187 /2 \pi C) - 2187 /2 \pi D) 2187 \pi = z cut by the cylinder Use Stokes' Theorem to calculate the circulation of the field F around the curve C in the indicated direction. -F = -9 i + 9 j + 4 k ; C: the portion of the paraboloid + = z cut by the cylinder A) - 2187 \pi B) 2187 /2 \pi C) - 2187 /2 \pi D) 2187 \pi


A) - 2187 π\pi
B) 2187 /2 π\pi
C) - 2187 /2 π\pi
D) 2187 π\pi

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q38: Find the surface area of the

Q39: Evaluate the surface integral of G

Q40: Find the work done by F

Q41: Use Stokes' Theorem to calculate the

Q42: Find the flux of the curl

Q44: Find the surface area of the surface

Q45: Evaluate the line integral along the curve

Q46: Find the flux of the vector

Q47: Evaluate the line integral of f(x,y)

Q48: Calculate the circulation of the field F