Multiple Choice
Find the volume of the indicated region.
-the region bounded by the paraboloid 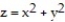 and the plane
and the plane 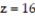
A) 
B) 64
C) 128
D) 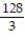
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q229: Evaluate the spherical coordinate integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg"
Q230: Find the center of mass of a
Q231: Find the volume under the surface
Q232: Find the center of mass of a
Q233: Use spherical coordinates to find the volume
Q235: Change the Cartesian integral to an
Q236: Change the order of integration and evaluate
Q237: Change the Cartesian integral to an
Q238: Find the average value of the function
Q239: Solve the problem.<br>-Find the average height of