Multiple Choice
Find the volume of the indicated region.
-the region bounded by the paraboloid 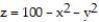 and the xy-plane
and the xy-plane
A) 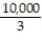
B) 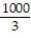
C) 500
D) 5000
Correct Answer:

Verified
Correct Answer:
Verified
Q158: Use cylindrical coordinates to find the
Q159: Find the area of the region
Q160: Use the given transformation to evaluate the
Q161: Find the average value of the
Q162: Find the average value of the function
Q164: Evaluate the cylindrical coordinate integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg"
Q165: Change the Cartesian integral to an equivalent
Q166: Solve the problem.<br>-Rewrite the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg"
Q167: Solve the problem.<br>-Set up the triple integral
Q168: Provide an appropriate response.<br>-What does the graph