Solved

Find the Center of Mass of a Thin Plate Covering

Question 195

Multiple Choice

Find the center of mass of a thin plate covering the given region with the given density function.
-The triangular region cut from the first quadrant by the line y = -x + 4, with density (x) = x


A) Find the center of mass of a thin plate covering the given region with the given density function. -The triangular region cut from the first quadrant by the line y = -x + 4, with density (x) = x A) B) C) D)
B) Find the center of mass of a thin plate covering the given region with the given density function. -The triangular region cut from the first quadrant by the line y = -x + 4, with density (x) = x A) B) C) D)
C) Find the center of mass of a thin plate covering the given region with the given density function. -The triangular region cut from the first quadrant by the line y = -x + 4, with density (x) = x A) B) C) D)
D) Find the center of mass of a thin plate covering the given region with the given density function. -The triangular region cut from the first quadrant by the line y = -x + 4, with density (x) = x A) 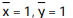B) 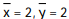C) 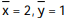D)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q190: Evaluate the integral by changing the order

Q191: Use the given transformation to evaluate the

Q192: Express the area of the region bounded

Q193: Find the volume of the indicated region.<br>-the

Q194: Evaluate the integral by changing the order

Q196: Use the given transformation to evaluate

Q197: Evaluate the improper integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the

Q198: Solve the problem.<br>-Find the average distance from

Q199: Choose the one alternative that best completes

Q200: Find the Jacobian for the given transformation<br>-<img