Solved

Solve the Problem. -Find the Center of Mass of the Region of Constant

Question 285

Multiple Choice

Solve the problem.
-Find the center of mass of the region of constant density bounded by the paraboloid Solve the problem. -Find the center of mass of the region of constant density bounded by the paraboloid and the xy-plane. A) B) C) D) and the xy-plane.


A) Solve the problem. -Find the center of mass of the region of constant density bounded by the paraboloid and the xy-plane. A) B) C) D)
B) Solve the problem. -Find the center of mass of the region of constant density bounded by the paraboloid and the xy-plane. A) B) C) D)
C) Solve the problem. -Find the center of mass of the region of constant density bounded by the paraboloid and the xy-plane. A) B) C) D)
D) Solve the problem. -Find the center of mass of the region of constant density bounded by the paraboloid and the xy-plane. A) 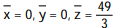B) 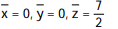C) 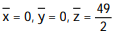D)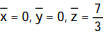

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q280: Express the area of the region bounded

Q281: Find the center of mass of a

Q282: Write an equivalent double integral with the

Q283: Find the center of mass of a

Q284: Write an equivalent double integral with the

Q286: Use the given transformation to evaluate the

Q287: Find the Jacobian for the given transformation<br>-<img

Q288: Solve the problem.<br>-Let D be the smaller

Q289: Evaluate the integral by changing the order

Q290: Evaluate the spherical coordinate integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg"