Solved

Solve the Problem. -Find the Center of Mass of a Tetrahedron of Density

Question 31

Multiple Choice

Solve the problem.
-Find the center of mass of a tetrahedron of density Solve the problem. -Find the center of mass of a tetrahedron of density bounded by the coordinate planes and the plane . A) B) C) D) bounded by the coordinate planes and the plane Solve the problem. -Find the center of mass of a tetrahedron of density bounded by the coordinate planes and the plane . A) B) C) D) .


A) Solve the problem. -Find the center of mass of a tetrahedron of density bounded by the coordinate planes and the plane . A) B) C) D)
B) Solve the problem. -Find the center of mass of a tetrahedron of density bounded by the coordinate planes and the plane . A) B) C) D)
C) Solve the problem. -Find the center of mass of a tetrahedron of density bounded by the coordinate planes and the plane . A) B) C) D)
D) Solve the problem. -Find the center of mass of a tetrahedron of density 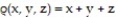bounded by the coordinate planes and the plane 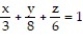. A) 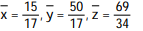B) 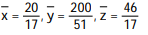C) 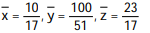D)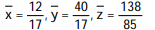

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q26: Find the center of mass of a

Q27: Solve the problem.<br>-Find the average height of

Q28: Evaluate the improper integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the

Q29: Solve the problem.<br>-Find the average height of

Q30: Find the volume of the indicated region.<br>-the

Q32: Evaluate the spherical coordinate integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg"

Q33: Change the Cartesian integral to an

Q34: Find the center of mass of the

Q35: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.

Q36: Choose the one alternative that best completes