Multiple Choice
At what points is the given function continuous?
-f(x, y) = 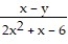
A) All (x, y) such that x  and x -2
and x -2
B) All (x, y)
C) All (x, y) such that x 0
D) All (x, y) satisfying x - y 0
Correct Answer:

Verified
Correct Answer:
Verified
Q53: Solve the problem.<br>-Find the derivative of the
Q54: Solve the problem.<br>-Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="
Q55: Find the limit.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Find the limit.
Q56: Solve the problem.<br>-Find the equation for the
Q57: Use implicit differentiation to find the specified
Q59: Find the limit.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Find the limit.
Q60: Solve the problem.<br>-Find the derivative of the
Q61: Find two paths of approach from which
Q62: Find the limit.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Find the limit.
Q63: Use implicit differentiation to find the specified