Solved

Find All the First Order Partial Derivatives for the Following

Question 31

Multiple Choice

Find all the first order partial derivatives for the following function.
-f(x, y, z) = z Find all the first order partial derivatives for the following function. -f(x, y, z) = z A) B) C) D)


A)
Find all the first order partial derivatives for the following function. -f(x, y, z) = z A) B) C) D)
B)
Find all the first order partial derivatives for the following function. -f(x, y, z) = z A) B) C) D)
C)
Find all the first order partial derivatives for the following function. -f(x, y, z) = z A) B) C) D)
D)
Find all the first order partial derivatives for the following function. -f(x, y, z) = z A) 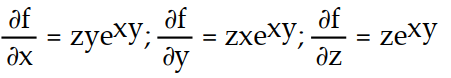B) 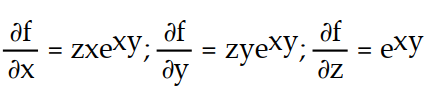C) 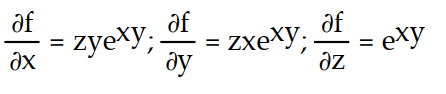D)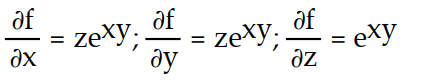

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q26: Solve the problem.<br>-Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Solve the

Q27: Sketch the surface z = f(x,y).<br>-f(x, y)

Q28: Sketch the surface z = f(x,y).<br>-f(x, y)

Q29: Use polar coordinates to find the limit

Q30: Find the derivative of the function at

Q32: Solve the problem. <br>-Find the least squares

Q33: Find the domain and range and describe

Q34: Solve the problem.<br>-Find the derivative of the

Q35: Solve the problem.<br>-Find the derivative of the

Q36: Find all the first order partial derivatives