Solved

Find a Function R(t) That Describes the Curve Where the Surfaces

Question 12

Multiple Choice

Find a function r(t) that describes the curve where the surfaces intersect.
-z = 16; z = Find a function r(t) that describes the curve where the surfaces intersect. -z = 16; z = + A) r(t) = B) r(t) = C) r(t) = D) r(t) = + Find a function r(t) that describes the curve where the surfaces intersect. -z = 16; z = + A) r(t) = B) r(t) = C) r(t) = D) r(t) =


A) r(t) = Find a function r(t) that describes the curve where the surfaces intersect. -z = 16; z = + A) r(t) = B) r(t) = C) r(t) = D) r(t) =
B) r(t) = Find a function r(t) that describes the curve where the surfaces intersect. -z = 16; z = + A) r(t) = B) r(t) = C) r(t) = D) r(t) =
C) r(t) = Find a function r(t) that describes the curve where the surfaces intersect. -z = 16; z = + A) r(t) = B) r(t) = C) r(t) = D) r(t) =
D) r(t) = Find a function r(t) that describes the curve where the surfaces intersect. -z = 16; z = 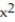+ A) r(t) = 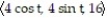B) r(t) = 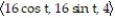C) r(t) = 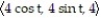D) r(t) =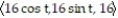

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q7: FInd the tangential and normal components

Q8: Find the unit tangent vector T and

Q9: Find the curvature of the space curve.<br>-r(t)

Q10: Compute the unit binormal vector and torsion

Q11: The position vector of a particle is

Q13: Find the length of the indicated

Q14: Find the curvature of the curve

Q15: Verify that the curve r(t) lies on

Q16: Find the length of the indicated

Q17: Find the length of the indicated