Multiple Choice
The position vector of a particle is r(t) . Find the requested vector.
-The acceleration at t = 
for r(t) = ( 9 sin 5t) i - ( 10 cos 5t) j + ( 2 csc 5t) k
A) a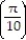 
= -225i - 50k
B) a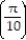 
= 225i + 50k
C) a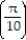 
= -225i + 50k
D) a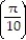 
= 250j + 50k
Correct Answer:
Verified
Correct Answer:
Verified
Related Questions
Q1: Find the unit tangent vector T and
Q3: Find the unit tangent vector T
Q4: Compute the unit binormal vector and torsion
Q5: Graph the curve described by the
Q6: The position vector of a particle is
Q7: FInd the tangential and normal components
Q8: Find the unit tangent vector T and
Q9: Find the curvature of the space curve.<br>-r(t)
Q10: Compute the unit binormal vector and torsion
Q11: The position vector of a particle is