Solved

Find the Curvature of the Curve R(t)

Question 33

Multiple Choice

Find the curvature of the curve r(t) .
-r(t) = ( 7 + cos 8t - sin 8t) i + ( 5 + sin 8t + cos 8t) j + 6k


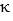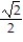
A) Find the curvature of the curve r(t) . -r(t) = ( 7 + cos 8t - sin 8t) i + ( 5 + sin 8t + cos 8t) j + 6k A) = B) = 4 C) = 4 D) = = Find the curvature of the curve r(t) . -r(t) = ( 7 + cos 8t - sin 8t) i + ( 5 + sin 8t + cos 8t) j + 6k A) = B) = 4 C) = 4 D) =
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 4
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11= 4 11ee9522_3542_c95c_bdb6_cb11aceb7be9_TB9662_11
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 11ee9522_3542_c95d_bdb6_53a201017f8b_TB9662_11

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q28: Evaluate the limit. <br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the

Q29: If r(t) is the position vector of

Q30: Find the unit tangent vector T and

Q31: The position vector of a particle is

Q32: Find the unit tangent vector of the

Q34: FInd the tangential and normal components of

Q35: Find the curvature of the curve r(t).<br>-r(t)

Q36: Compute r''(t).<br>-r(t) = (cos 2t)i + (

Q37: Find the unit tangent vector T and

Q38: Compute the unit binormal vector and torsion