Solved

Find the Magnitude of U × V and the Unit

Question 81

Multiple Choice

Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v.
-u = 2i + 2j - k, v = -i + k


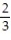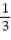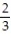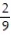A) 3; Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v. -u = 2i + 2j - k, v = -i + k A) 3; i + j - k B) 9; i + j - k C) 3; i - j + k D) 9; i - j + k i + Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v. -u = 2i + 2j - k, v = -i + k A) 3; i + j - k B) 9; i + j - k C) 3; i - j + k D) 9; i - j + k j - Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v. -u = 2i + 2j - k, v = -i + k A) 3; i + j - k B) 9; i + j - k C) 3; i - j + k D) 9; i - j + k k
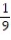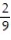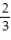B) 9; Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v. -u = 2i + 2j - k, v = -i + k A) 3; i + j - k B) 9; i + j - k C) 3; i - j + k D) 9; i - j + k i + Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v. -u = 2i + 2j - k, v = -i + k A) 3; i + j - k B) 9; i + j - k C) 3; i - j + k D) 9; i - j + k j - Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v. -u = 2i + 2j - k, v = -i + k A) 3; i + j - k B) 9; i + j - k C) 3; i - j + k D) 9; i - j + k k
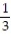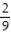C) 3; Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v. -u = 2i + 2j - k, v = -i + k A) 3; i + j - k B) 9; i + j - k C) 3; i - j + k D) 9; i - j + k i - Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v. -u = 2i + 2j - k, v = -i + k A) 3; i + j - k B) 9; i + j - k C) 3; i - j + k D) 9; i - j + k j + Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v. -u = 2i + 2j - k, v = -i + k A) 3; i + j - k B) 9; i + j - k C) 3; i - j + k D) 9; i - j + k k
D) 9; Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v. -u = 2i + 2j - k, v = -i + k A) 3; i + j - k B) 9; i + j - k C) 3; i - j + k D) 9; i - j + k i - Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v. -u = 2i + 2j - k, v = -i + k A) 3; i + j - k B) 9; i + j - k C) 3; i - j + k D) 9; i - j + k j + Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v. -u = 2i + 2j - k, v = -i + k A) 3; i + j - k B) 9; i + j - k C) 3; i - j + k D) 9; i - j + 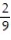k k

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q76: Determine whether the following is always true

Q77: Write the equation for the plane.<br>-The plane

Q78: Solve the problem.<br>-A force of magnitude

Q79: Find the triple scalar product (u x

Q80: Solve the problem.<br>-Find the area of the

Q82: Match the equation with the surface it

Q83: Solve the problem.<br>-For the triangle with

Q84: Identify the surface by name.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Identify

Q85: Write the equation for the plane.<br>-The plane

Q86: Determine whether the pairs of lines are