Identify the Quadric Surface by Name

Multiple Choice

Identify the quadric surface by name. Find and describe the xy-, xz-, and yz-traces, when they exist.
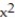--9 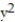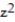- 9 + = 9

A) Ellipsoid; xy-trace: -9x² - 9y² = 9 (circle) ; xz-trace: z² - 9 x² = 9 (ellipse) ; yz-trace: z² - 9 y² = 9 (ellipse)

B) Hyperboloid of two sheets; xy-trace: -9x² - 9y² = 9(circle) ; xz-trace: z² - 9 x² = 9 (hyperbola) ; yz-trace: z² - 9 y² = 9 (hyperbola)

C) Hyperboloid of two sheets; xz-trace: z² - 9 x² = 9 (hyperbola) ; yz-trace: z² - 9 y² = 9(hyperbola)

D) Hyperboloid of one sheet; xy-trace: -9x² - 9y² = 9 (circle) ; xz-trace: z² - 9 y² = 9 (hyperbola) ; yz-trace: z² - 9y² = 9 (hyperbola)