Multiple Choice
Calculate the arc length of the indicated portion of the curve r(t) .
-r(t) = ( 7 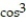 2t) j + ( 7
2t) j + ( 7 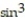 2t) k;
2t) k; 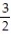 t
t 
A) 0
B) 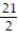
C) 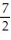
D) 21
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q62: Find the length of the curve.<br>-The
Q63: Find the area of the specified
Q64: Find a parametrization for the curve.<br>-The line
Q65: Find the length of the curve.<br>-The
Q66: Find the standard-form equation of the hyperbola
Q68: Find the Cartesian coordinates of the given
Q69: Find a parametrization for the curve.<br>-The upper
Q70: Find the focus and directrix of the
Q71: Replace the polar equation with an
Q72: Find the standard-form equation of the ellipse