Multiple Choice
Find the area of the specified region.
-Inside the circle r = a sin and outside the cardioid r = a(1 - sin ) , a > 0
A) 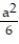 (4 - 3
(4 - 3 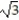 )
)
B) 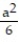 (6 - )
(6 - )
C) 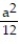 (2 - 3
(2 - 3 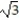 )
)
D) 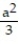 (3
(3 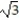 - )
- )
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q14: Find the focus and directrix of the
Q15: Determine if the given polar coordinates
Q16: Graph. <br>-9 <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Graph. -9
Q17: Find the length of the curve.<br>-The
Q18: Replace the polar equation with an
Q20: Graph the pair of parametric equations
Q21: Determine if the given polar coordinates
Q22: Plot the point whose polar coordinates are
Q23: Find the standard-form equation of the hyperbola
Q24: Graph the parabola or ellipse. Include the