Solved

Find the Linear Approximating Polynomial for the Function Centered at A

Question 24

Multiple Choice

Find the linear approximating polynomial for the function centered at a.
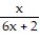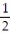-f(x) = Find the linear approximating polynomial for the function centered at a. -f(x) = , a = 0 A) L(x) = x B) L(x) = x C) L(x) = - x D) L(x) = - x , a = 0


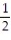A) L(x) = Find the linear approximating polynomial for the function centered at a. -f(x) = , a = 0 A) L(x) = x B) L(x) = x C) L(x) = - x D) L(x) = - x x
B) L(x) = Find the linear approximating polynomial for the function centered at a. -f(x) = , a = 0 A) L(x) = x B) L(x) = x C) L(x) = - x D) L(x) = - x x
C) L(x) = - Find the linear approximating polynomial for the function centered at a. -f(x) = , a = 0 A) L(x) = x B) L(x) = x C) L(x) = - x D) L(x) = - x x
D) L(x) = - Find the linear approximating polynomial for the function centered at a. -f(x) = , a = 0 A) L(x) = x B) L(x) = x C) L(x) = - x D) L(x) = - x x

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q19: Find the first four terms of the

Q20: Find the linear approximating polynomial for the

Q21: Use Taylor series to evaluate the limit.<br>-<img

Q22: Find the first four terms of the

Q23: Find the quadratic approximation of f at

Q25: Use power series operations to find the

Q26: Use power series operations to find the

Q27: Find the function represented by the power

Q28: Use power series operations to find the

Q29: Find the quadratic approximation of f at