Solved

Find the Quadratic Approximation of F at X = 0

Question 40

Multiple Choice

Find the quadratic approximation of f at x = 0.
-f(x) = sin ln( 2x + 1)


A) Q(x) = 1 + 2x + 2 Find the quadratic approximation of f at x = 0. -f(x) = sin ln( 2x + 1) A) Q(x) = 1 + 2x + 2 B) Q(x) = 2x - 2 C) Q(x) = 2x + 2 D) Q(x) = 1 - 2x + 2
B) Q(x) = 2x - 2 Find the quadratic approximation of f at x = 0. -f(x) = sin ln( 2x + 1) A) Q(x) = 1 + 2x + 2 B) Q(x) = 2x - 2 C) Q(x) = 2x + 2 D) Q(x) = 1 - 2x + 2
C) Q(x) = 2x + 2 Find the quadratic approximation of f at x = 0. -f(x) = sin ln( 2x + 1) A) Q(x) = 1 + 2x + 2 B) Q(x) = 2x - 2 C) Q(x) = 2x + 2 D) Q(x) = 1 - 2x + 2
D) Q(x) = 1 - 2x + 2 Find the quadratic approximation of f at x = 0. -f(x) = sin ln( 2x + 1) A) Q(x) = 1 + 2x + 2 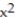B) Q(x) = 2x - 2 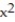C) Q(x) = 2x + 2 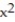D) Q(x) = 1 - 2x + 2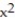

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q35: Find the interval of convergence of

Q36: Find the first four nonzero terms in

Q37: Determine the radius of convergence of

Q38: Find the series' radius of convergence.<br>-<img

Q39: Use Taylor series to evaluate the limit.<br>-<img

Q41: Find the first four nonzero terms in

Q42: Find the quadratic approximation of f at

Q43: Find the Taylor series generated by f

Q44: Find the Taylor polynomial of order 3

Q45: Solve the problem.<br>-Use a Taylor series to