Solved

Use Power Series Operations to Find the Taylor Series at X

Question 53

Multiple Choice

Use power series operations to find the Taylor series at x = 0 for the given function.
-f(x) = 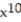Use power series operations to find the Taylor series at x = 0 for the given function. -f(x) = sin x A) B) C) D) sin x


A)
Use power series operations to find the Taylor series at x = 0 for the given function. -f(x) = sin x A) B) C) D)
B)
Use power series operations to find the Taylor series at x = 0 for the given function. -f(x) = sin x A) B) C) D)
C)
Use power series operations to find the Taylor series at x = 0 for the given function. -f(x) = sin x A) B) C) D)
D)
Use power series operations to find the Taylor series at x = 0 for the given function. -f(x) = sin x A) 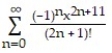B) 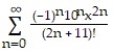C) 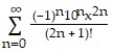D)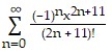

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q48: Find the Taylor series generated by f

Q49: Find the quadratic approximation of f at

Q50: Find the Taylor polynomial of order 3

Q51: Solve the problem.<br>-Use a Taylor series to

Q52: Use Taylor series to evaluate the limit.<br>-<img

Q54: Find the series' radius of convergence.<br>-<img

Q55: Find the series' radius of convergence.<br>-<img

Q56: Find the quadratic approximation of f at

Q57: Find the series' radius of convergence.<br>-<img

Q58: Find the Taylor series generated by f