Multiple Choice
Consider the boundary value problem
-  = f(x) , 0 < x < 1, y(0) = 0,
= f(x) , 0 < x < 1, y(0) = 0, 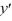 (1) = 0
(1) = 0
Which of these is the Green's function representation of the solution of the given boundary value problem?
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Q1: Consider the boundary value problem<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q2: Consider the boundary value problem<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q4: Consider the Sturm-Liouville problem<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider the
Q5: Consider the boundary value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q6: Consider the eigenfunction problem<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider the
Q7: Consider the boundary value problem<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q8: Determine the eigenfunctions for the eigenvalue problem<br>
Q9: Consider the eigenfunction problem<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q10: Consider the boundary value problem<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q11: Consider the eigenfunction problem<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider