Multiple Choice
What is the solution of the following initial boundary value problem?
4 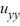 =
= 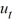 , u(0, t) = 0, u(2, t) = 0, u(x, 0) = sin(4?x)
, u(0, t) = 0, u(2, t) = 0, u(x, 0) = sin(4?x)
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Q28: The ends of a rod 75 cm
Q29: Consider the following periodic function with period
Q30: Consider the following periodic function with period
Q31: Consider the boundary value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q32: Suppose f (x) is defined by f
Q34: Consider the boundary value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q35: Consider the following periodic function with period
Q36: Consider the following periodic function with period
Q37: Consider the following periodic function with period
Q38: For which of these partial differential