Consider This Competing Species Model:

Which of the Following $\left(-\frac{1}{3}, \frac{5}{3}\right)$

Multiple Choice

Consider this competing species model: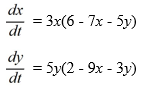

Which of the following statements are true? Select all that apply.

A) The entire first quadrant is the basin of attraction for the critical point $\left(-\frac{1}{3}, \frac{5}{3}\right)$ .
B) The origin is an unstable node.
C) Both $\left(-\frac{6}{7}, 0\right)$ and $\left(-\frac{2}{3}, 0\right)$ are saddle points.
D) Both $\left(\frac{6}{7}, 0\right)$ and $\left(0, \frac{2}{3}\right)$ are saddle points
E) All solution trajectories approach the origin as $t \rightarrow \infty$ .
F) The critical point $\left(-\frac{1}{3}, \frac{5}{3}\right)$ corresponds to coexistence in this model.