Multiple Choice
Suppose ? is a positive real parameter. Consider this competing species model: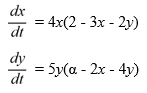
Which of these are critical points for this system? Select all that apply.
A)
B)
C)
D)
E)
F)
G)
H)
I)
Correct Answer:

Verified
Correct Answer:
Verified
Q23: Consider the linear system <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q24: Consider the linear system <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q25: Find an equation of the form H(x,
Q26: Consider the linear system <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q27: Consider the following nonlinear system:<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q29: Consider the linear system <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q30: Consider the linear system <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q31: Suppose α is a positive real parameter.
Q32: Consider the linear system <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q33: Find an equation of the form