Multiple Choice
Consider the following nonlinear system: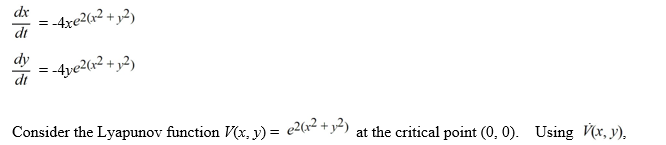
What can you conclude about this nonlinear system?
A) The origin is asymptotically stable.
B) The origin is an unstable node.
C) The basin of attraction for the origin is the entire xy-plane.
D) The origin is a center and all solution trajectories encircle it.
Correct Answer:

Verified
Correct Answer:
Verified
Q41: For which of the following systems
Q42: Consider the following nonlinear system expressed in
Q43: Consider the following nonlinear system:<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q44: Consider the van der Pol equation <img
Q45: Consider the linear system <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q47: Suppose ? is a real parameter.
Q48: Consider the following nonlinear system expressed in
Q49: Consider the linear system <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q50: Consider the linear system <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q51: Consider the following nonlinear system:<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"