Consider the Initial Value Problem This Question Relates to Using

Multiple Choice

Consider the initial value problem 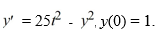This question relates to using the backward Euler method to approximate the solution at t = 0.4, namely = y(0.4) , using a step size of h = 0.02.
Which of these equations is the result of applying the backward Euler method to solve for

A) $y_{1}^{2}-y_{1}+25 \times 0.4^{2}=0$
B) $0.02 y_{1}^{2}+y_{1}-\left(1+25 \times 0.4^{2} \times 0.02\right) =0$
C) $0.02 y_{1}^{2}-y_{1}+\left(1+25 \times 0.4^{2} \times 0.02\right) =0$
D) $y_{1}^{2}+y_{1}-25 \times 0.4^{2}=0$