Multiple Choice
Consider the first-order nonhomogeneous initial value problem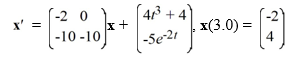
Given a fundamental matrix 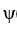 (t) for the system, what is the solution of this initial value problem?
(t) for the system, what is the solution of this initial value problem?
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Q77: Consider the first-order homogeneous system of
Q78: Suppose Tank A contains 50 gallons of
Q79: Consider the first-order homogeneous system of linear
Q80: Consider the first-order homogeneous system of
Q81: Consider the first-order homogeneous system of linear
Q83: Consider the first-order homogeneous system of
Q84: Consider the first-order homogeneous system of
Q85: Consider the first-order nonhomogeneous initial value
Q86: Consider the first-order homogeneous system of
Q87: Consider these matrices:<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider these